Planning and Optimisation:
a use case with OR-Tools and FlexSim for AGV fleets
This paper addresses how the integration between FlexSim and Google OR-Tools could optimise the assignment of missions to AGVs, demonstrating the potential of FlexSim in dealing with complex problems through advanced and customisable solutions. Whether you want to find out how to optimise your AGV fleet or learn more about our customised solutions for your business, contact us.
Google OR-Tools (Optimisation Tools) is an open-source suite developed by Google for solving optimisation problems. It is particularly useful for addressing complex optimisation problems such as planning and scheduling. These include determining the efficient allocation of resources, time, and priorities. Moreover, it is used for tasks like route planning, bin-packing, and more.
This suite is compatible with several programming languages, including Python. Thanks to the connection between FlexSim and Python, we can take advantage of Google’s OR-Tools to optimise the assignment of a series of missions to a fleet of AGVs. One of the advantages of OR-Tools is the possibility to optimise the Vehicle Routing Problem (VRP). This tool makes it possible to plan the routes of a set of vehicles to deliver goods or services to a group of customers. This reduces costs such as distance travelled, time or fuel. Finally, the system ensures compliance with any constraints.
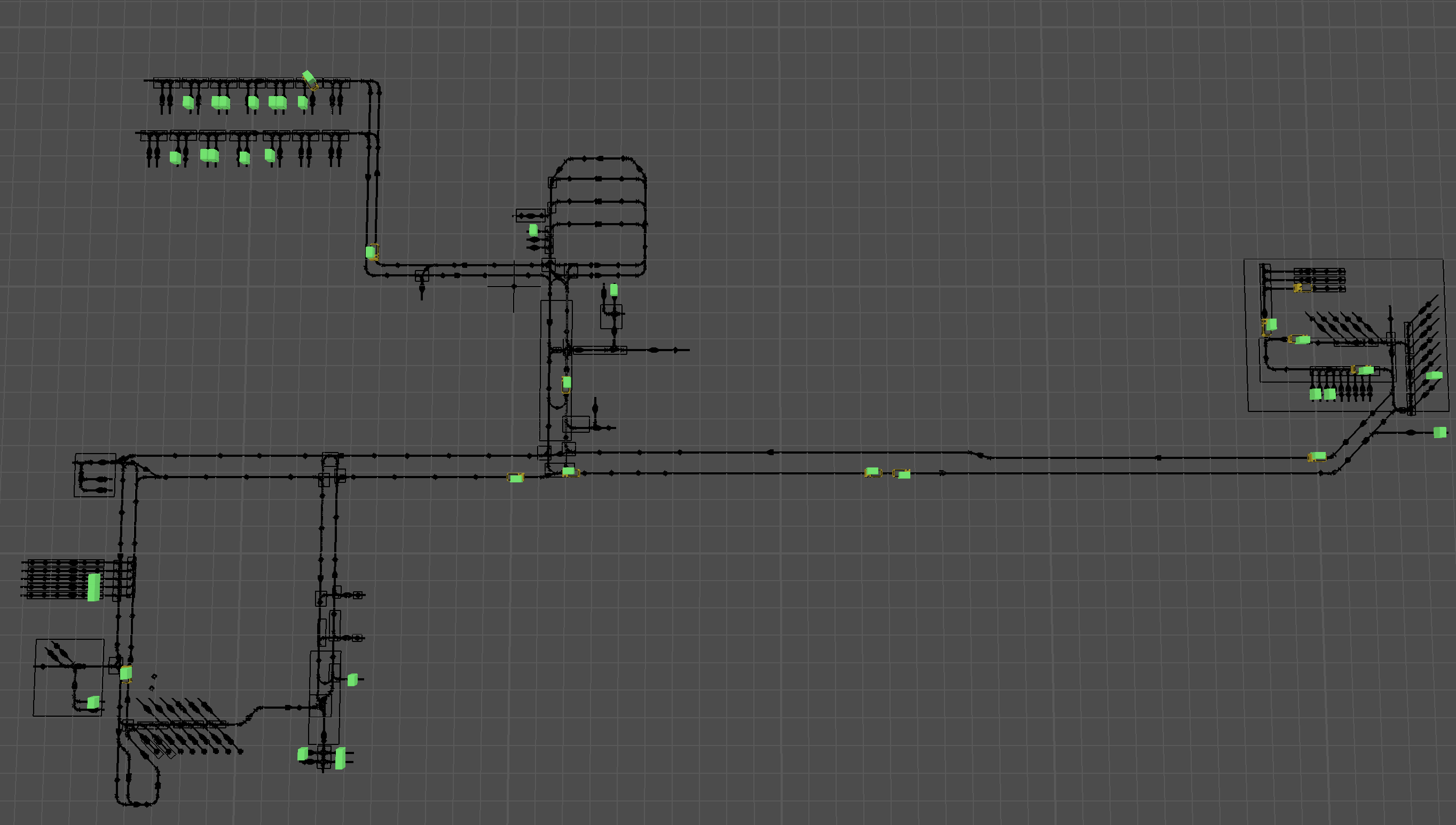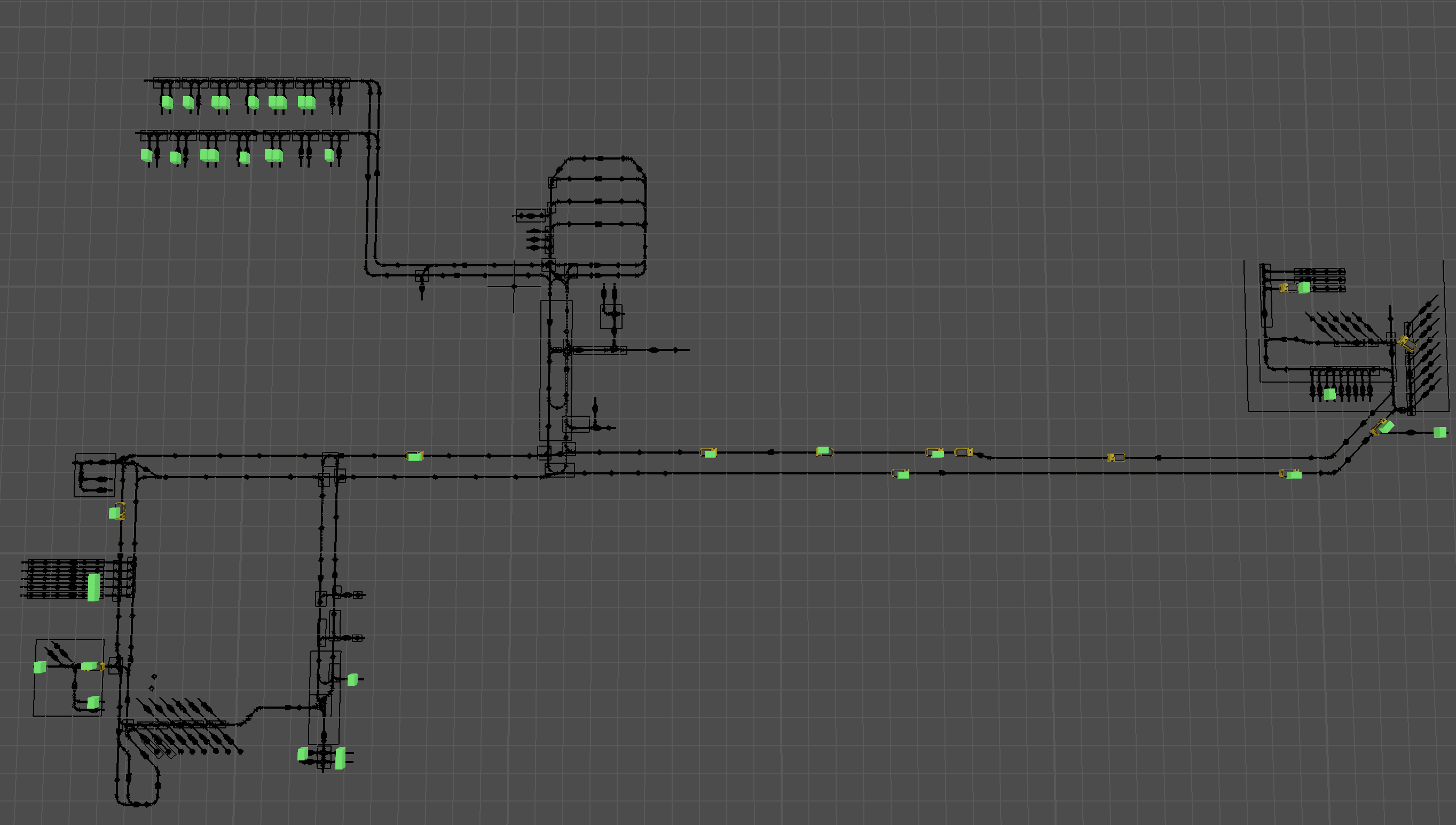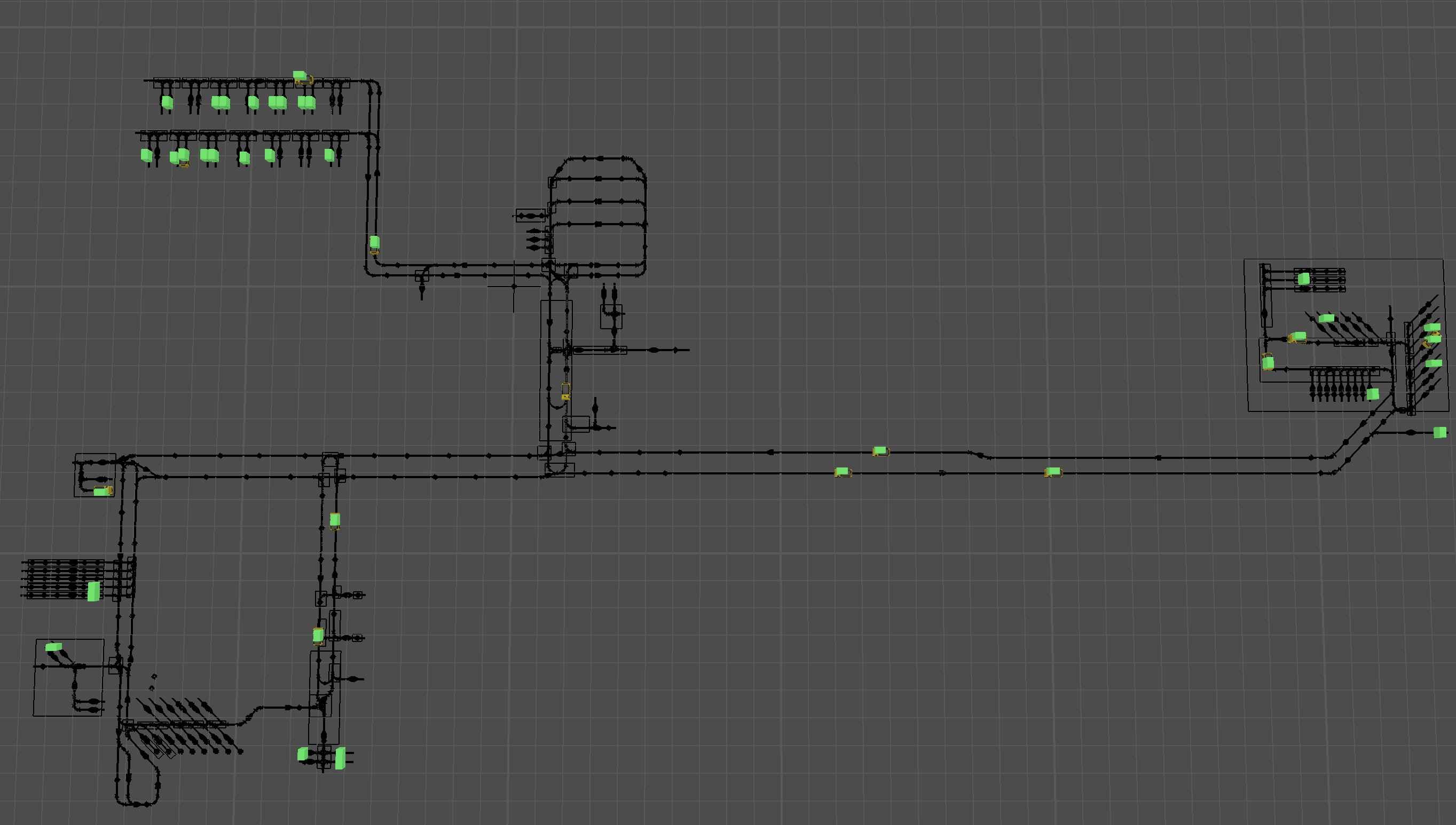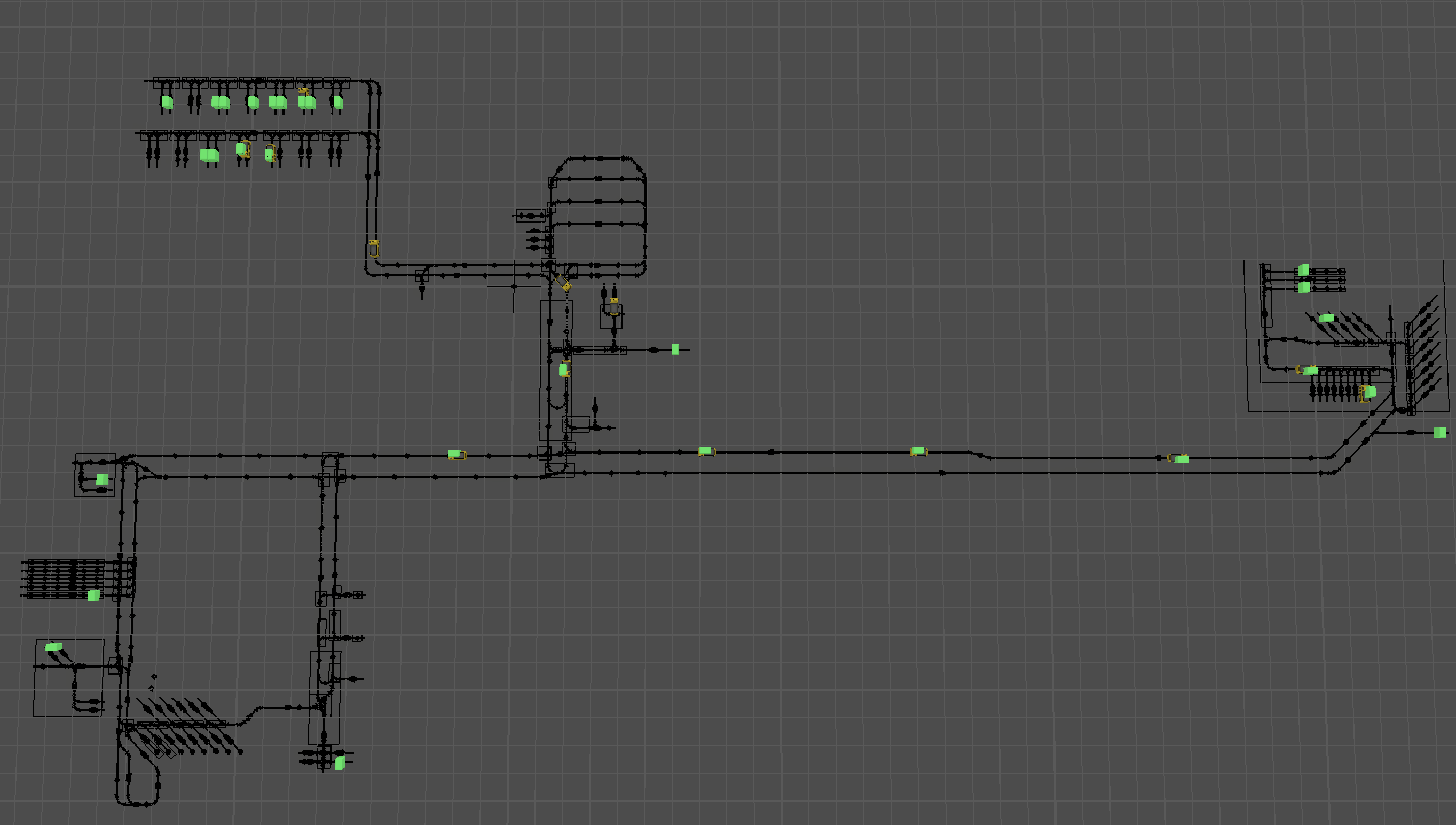
Optimisation of AGV fleets with FlexSim and OR-Tools in the simulation model
In the simulation model developed in FlexSim, we have a fleet of AGVs. These AGVs pick up products at specific points on the AGV network. Then, they transport the products to their destinations, which are an equal number of points also located on the network.
Products are generated at random time slots and the origin and destination points of the goods are randomly assigned. OR-Tools’ VRP solver is used as a method to distribute pick and delivery tasks to our vehicles.
In the classic VRP, we have a depot from which all vehicles depart to serve a series of customers and then return to the depot. The VRP can be described using a graph made up of a set of nodes and arcs. The nodes represent the customers to be reached by the vehicles and the arcs represent the possible connections. The goal of the solver is to find the best routes that minimise the total cost (in our case the distance travelled).
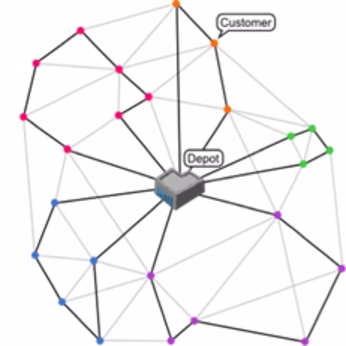
Adapting the AGV problem to OR-Tools
In the FlexSim model, we do not have a true common storage point for all vehicles. In fact, since picking/delivery missions are assigned ‘on the fly’ as soon as the products are generated, the AGVs start performing missions from the point in the network where they are when the task is created and assigned.
Furthermore, since we are using AGVs with a transport capacity of one product at a time, the AGV will pick up the product and take it directly to its destination, requiring node sorting.
Therefore, it was necessary to adapt the AGV problem to a format that can be solved by OR-Tools.
Specifically, the position that the AGV occupies on the network represents a node in the graph representation of the VRP. Similarly, the point where the AGV completes the picking/delivery task is also comparable to a node. Since the VRP assumes a common depot for all vehicles, in FlexSim the distance from the AGV’s location and the depot (at the time the task is assigned to the AGV) is treated as zero. As a result, the cost associated with the distance between the AGV’s location and the depot is effectively null.
In this way, we allow the AGV to start performing the task from any point on the network without incurring additional costs. However, we impose the constraint that the AGV must pass through the node corresponding to its current position.
Simplifying the problem for OR-Tools
Since the AGV must immediately deliver a product as soon as it is picked up, each picking/delivery task is treated as a single node in the graph representation of the VRP, rather than having two separate nodes corresponding to the pickup and delivery points. This simplifies the problem that the solver needs to address.
The cost of moving from a point on the AGV network to the task node considers multiple factors. It takes into account both the distance to reach the pick-up point and the distance between the pick-up point and the delivery point.
After adapting the FlexSim model to make it solvable via the OR-Tools solver and after testing the dispatching rule provided by the solver, we compared it with two other possible dispatching modes:
- The “Closest” mode, where the AGV, once free, selects the next task whose pickup point is closest to its current position;
- The “FIFO” (First In First Out) mode, which assigns tasks based on their order of arrival.
By using the Experimenter in FlexSim, we can carry out numerous what-if scenarios. This allows us to compare various KPIs (Key Performance Indicators). The comparison is made by varying both the dispatching strategies and the number of tasks to be performed per hour. Specifically, the following KPIs were analyzed:
AvgTaskTime
This metric measures the total time an AGV needs to complete a picking/delivery mission. We analyse the time from the moment the task is assigned to the delivery of the product.

The VRP solver demonstrated excellent performance in low-demand scenarios. In fact, strategies like “Closest” and FIFO, when applied to low-demand scenarios with many idle AGVs, tend to assign tasks to any available AGV. However, these AGVs may need to travel long distances to complete the task, resulting in increased time. In contrast, the VRP solver aims to minimize the distance traveled. It then waits and assigns the mission to an AGV that will be closer to the picking point, leaving more distant AGVs idle.
AvgWorkStaytime (Product stay time in the system)
This metric measures the total time a product spends in the system, from its creation to its delivery. Essentially, it tracks how long a product “waits” before moving to its destination.

The “Closest” strategy outperformed the VRP solver for this metric. Although counterintuitive, we can explain it by the VRP solver’s focus on minimizing the distance traveled by AGVs. This optimization may delay the assignment of some tasks to reduce the overall distance. As a result, it increases the product stay time before delivery. Additionally, the solver continually reanalyzes the system state and recalculates the optimal solution whenever a new product is generated. As a result, the system may deliver products generated earlier later than those generated more recently.
AvgAGVUtilization
This metric evaluates how efficiently the system has deployed the AGVs.
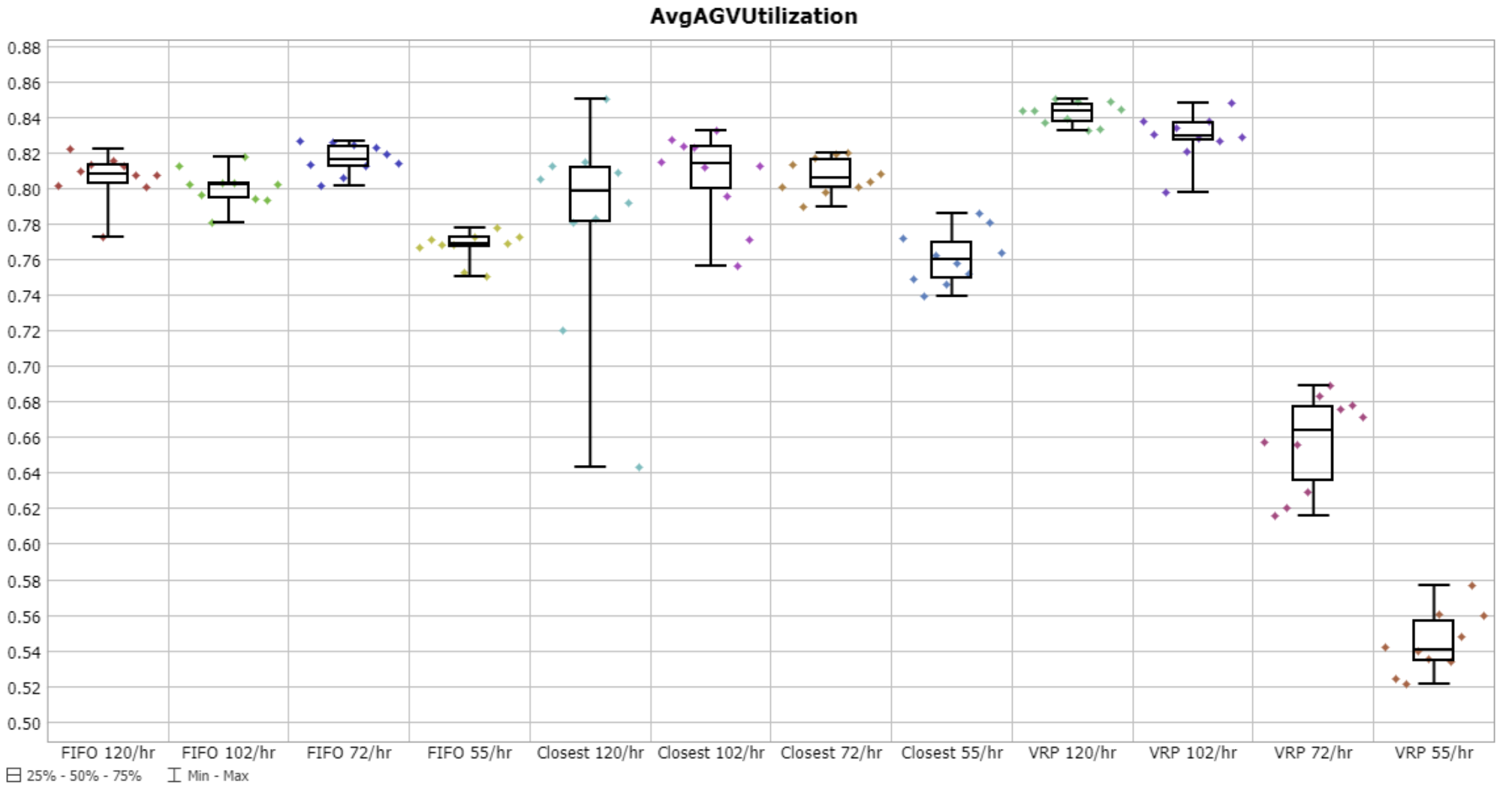
In low-demand scenarios, VRP solver demonstrated excellent optimization capabilities by keeping some AGVs inactive until strictly necessary, thus reducing empty trips. On the other hand,
On the other hand, the ‘Closest’ and ‘FIFO’ strategies immediately commit an idle AGV as soon as an unassigned mission arrives. However, in many cases, it might be more efficient to wait for an AGV closer to the task node to become available, before assigning it.
ThroughputPerHour
This metric indicates the number of tasks completed per hour, measuring the AGVs’ ability to handle the workflow efficiently.
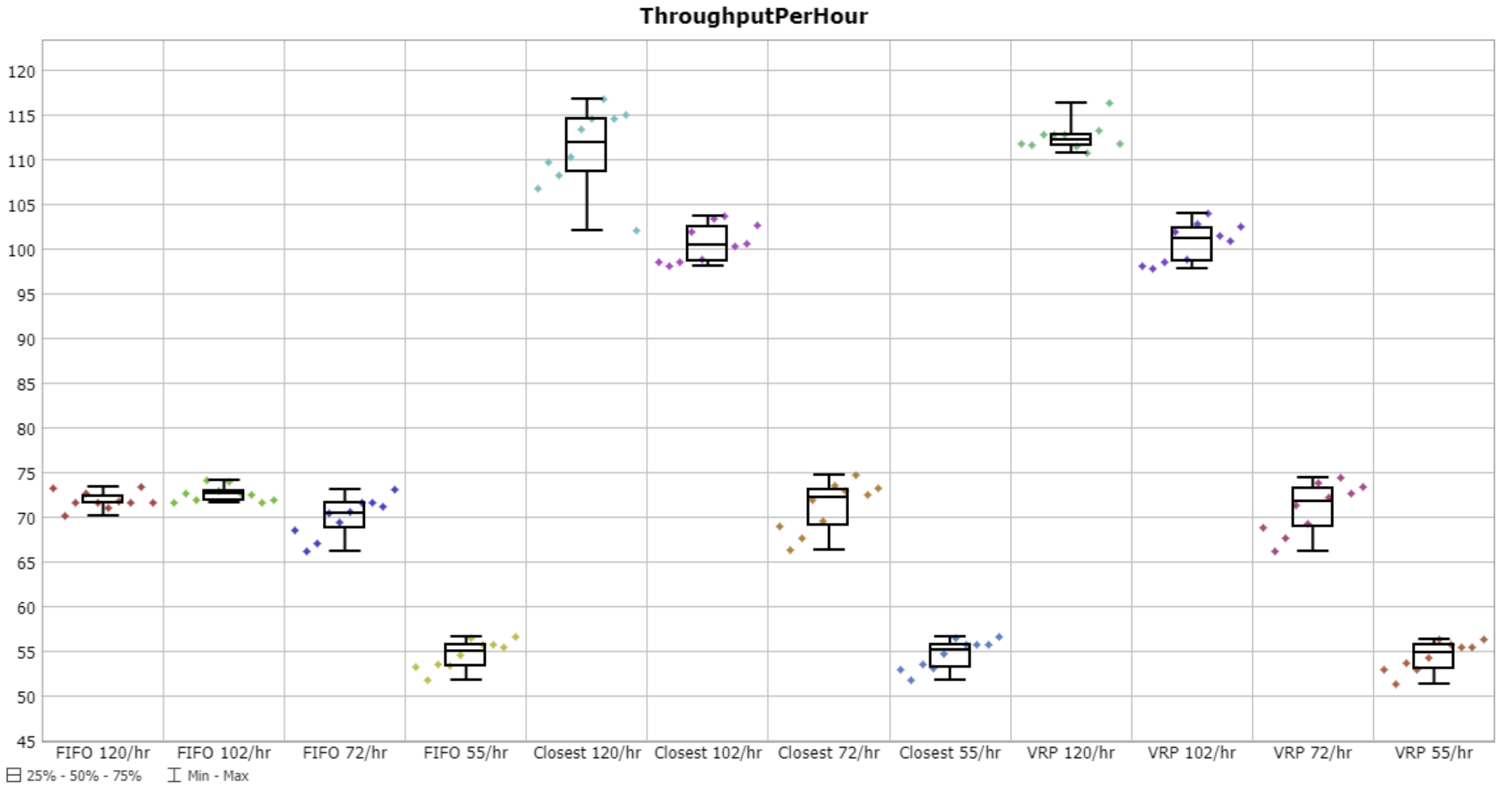
If the system managed the volume of missions properly, the average throughput would match the number of queries per hour. In high-demand scenarios, both the VRP solver and the ‘Closest’ strategy fail to fully handle the entire workload. On the other hand, the FIFO strategy showed the worst performance due to accumulated delays.
Applications
The optimization of AGV tasks using FlexSim and OR-Tools showcases how to fully leverage FlexSim’s potential to address complex problems with scalable and customizable solutions.
This solution offers versatility. It applies to various production environments, such as assembly lines, internal logistics, automated warehouses, geographical-scale freight transport. Additionally, it addresses many other industrial and logistical needs.
Contact Flexcon to access the free model featured in this article and discover more about FlexSim.
